آموزش معادلات دیفرانسیل همگن (گام به گام با مثال)
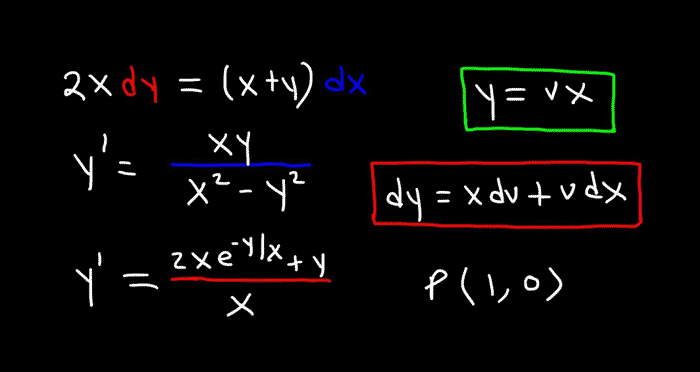
در این مطلب آموزش معادلات دیفرانسیل همگن (به انگلیسی homogeneous differential equation) به زبان ساده خواهیم داشت. یک تابع f(x,y) در واقع یک تابع همگن است که اگر به این صورت باشد:
![]()
در این معادله یک عدد حقیقی است. هر معادله دیفرانسیلی به فرم f(x,y)dy=g(x,y)dx یک معادله دیفرانسیل همگن است؛ البته اگر f(x,y) و g(x,y) از یک درجه باشند.
یک معادله همگن رفتار مقیاس پذیری ضربی از خودش نشان می دهد. این یعنی اگر همه عبارت های آن در یک ضریب ضرب شوند، مقدار کل تابع در توانی از آن مضرب ضرب می شود.
در کنار این مطلب یاد بگیرید: آموزش مشتقات جزئی ریاضی مهندسی با مثال
معادلات دیفرانسیل همگن
از نظر ریاضی، می توان گفت که یک معادله دیفرانسیل مشخص اگر تابعی همگن داشته باشد، همگن است. از طرفی هم یک تابع همگن تابعی به این صورت است که در آن لامبدا یا 𝜆یک ثابت غیر صفر است:
![]()
به طور کلی، می توانیم یک معادله دیفرانسیل همگن را به صورت f(x, y).dy + g(x,y).dx = 0 بنویسیم. همچنین باید توجه داشته باشیم که در یک معادله دیفرانسیل همگن درجه x و y در کل معادله ثابت می ماند.
نکته: معادله دیفرانسیل همگن به صورت زیر نوشته می شود:
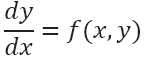
و یک تابع همگن به این صورت:
![]()
انواع معادلات دیفرانسیل همگن
در ادامه انواع معادلات دیفرانسیل همگن را تعریف خواهیم کرد .
معادلات دیفرانسیل خطی همگن
در این نوع معادلات دیفرانسیل، هر جمله به شکل ![]() است که یعنی مشتق y ضرب در تابع x. به طور کلی، حل چنین معادلات دیفرانسیل خطی بسیار دشوار است اما اگر تمام ضرایب ثابت باشند، می توان به جواب های دقیق تری رسید.
است که یعنی مشتق y ضرب در تابع x. به طور کلی، حل چنین معادلات دیفرانسیل خطی بسیار دشوار است اما اگر تمام ضرایب ثابت باشند، می توان به جواب های دقیق تری رسید.
یک معادله دیفرانسیل خطی همگن این گونه است:
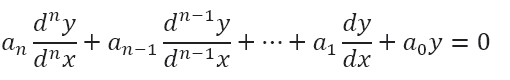
که در آن ![]() ثابت اند و کل تابع شبیه یک چند جمله ای است.
ثابت اند و کل تابع شبیه یک چند جمله ای است.
حتما دانلود کنید: آموزش صفر تا صد زبان انگلیسی با 32 درس رایگان
معادلات دیفرانسیل جزئی همگن
معادله دیفرانسیل جزئی که معمولا به عنوان PDE شناخته می شود، نوعی معادله دیفرانسیل است که مشتقات جزئی متغیر وابسته را شامل می شود. تابع یک معادله دیفرانسیل جزئی به صورت زیر نوشته می شود:
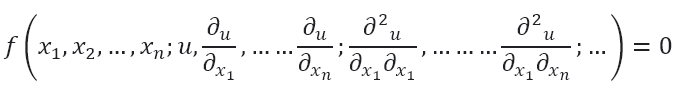
که در آن ![]() یک تابع است.
یک تابع است.
اگر تمام عبارات یک PDE دارای متغیر وابسته یا مشتقات جزئی آن باشند، ناهمگن است، در غیر این صورت یک دیفرانسیل جزئی همگن است.
برخی از نمونه های معادلات دیفرانسیل جزئی همگن عبارتند از:
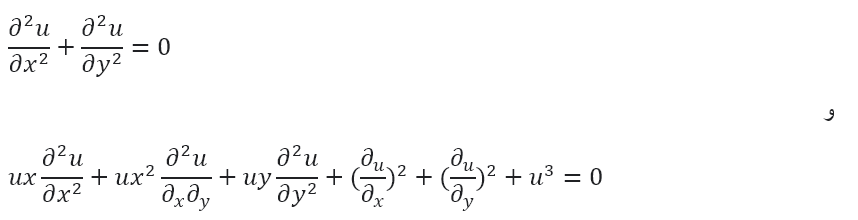
معادلات دیفرانسیل همگن مرتبه اول
یک معادله دیفرانسیل همگن مرتبه اول به شکل y’+p(t)y=0 است.
این که در این معادله دیفرانسیل، y و y’ به صورت مرتبه اول می آیند، یعنی خطی است.
و وجود صفر در سمت راست معادله نشان دهنده همگن بودن آن است.
از آن جایی که این معادلات دیفرانسیل قابل تفکیک هستند، می توانیم آن ها را با روش های ساده حل کنیم:

در این جا P(t) ضد مشتق یا انتگرال p(t) است.
حتما بخوانید: نکات عمومی و پیشرفته ریاضی در نرم افزار متلب
معادلات دیفرانسیل همگن مرتبه دوم
معادله دیفرانسیل همگن مرتبه دوم یک نوع اصلی از معادلات دیفرانسیل مرتبه دوم با دو ضریب مهم است:
یک معادله دیفرانسیل مرتبه دوم باید حداکثر دارای یک عبارت دیفرانسیل توان دو باشد.
این معادله زمانی همگن است که اگر تمام عبارت ها به یک طرف آورده شوند، طرف دیگر در نهایت صفر شود.
با توجه به دو نکته فوق، یک معادله دیفرانسیل همگن مرتبه دوم را می توان به صورت زیر نوشت:
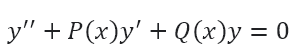
یا
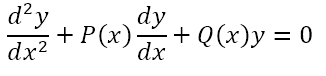
معادله دیفرانسیل همگن مرتبه دوم بیشتر به شکل زیر نوشته می شود:
![]()
که در آن a و b و c ثابت هستند.
a برابر با صفر نیست.
مراحل حل معادلات دیفرانسیل همگن
با انتگرال گرفتن از معادله دیفرانسیل داده شده می توانیم جواب معادلات دیفرانسیل همگن را به دست بیاوریم. هر معادله دیفرانسیل همگن فرم ![]() را می توان با جدا کردن متغیر ها و مشتقات آن ها در هر دو طرف و سپس انتگرال گیری نسبت به متغیر حل کرد .
را می توان با جدا کردن متغیر ها و مشتقات آن ها در هر دو طرف و سپس انتگرال گیری نسبت به متغیر حل کرد .
برای حل معادلات دیفرانسیل همگن این طور در نظر می گیریم که y=v.x است. این جایگزینی حل معادله و انتگرالگیری را آسان می کند.
با مشتق گیری از y=v.x نسبت به x، چنین چیزی خواهیم داشت :
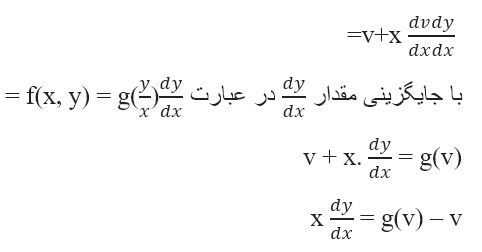
و با جدا کردن متغیر های x و v، داریم:
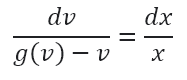
با انتگرال گیری در هر دو طرف:
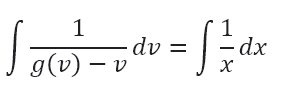
و حل عبارت فوق، به چنین جوابی می رسیم:
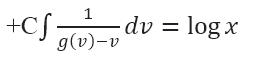
حالا مقدار ![]() را جایگزین می کنیم تا جواب کلی معادله دیفرانسیل را بدست بیاوریم.
را جایگزین می کنیم تا جواب کلی معادله دیفرانسیل را بدست بیاوریم.
بلد باشید: آموزش تایپ ریاضی در ورد (و 5 نکته)
تفاوت بین معادلات دیفرانسیل همگن و غیرهمگن
یک معادله دیفرانسیل همگن شامل مشتقات y و عبارات مربوط به y و برابر با صفر است . در حالی که یک معادله دیفرانسیل ناهمگن شبیه معادلات همگن است تنها با این تفاوت که عبارت های حاوی x و سایر ثابت ها می توانند در سمت راست معادله باشند .
دانلود کنید: آموزش ریاضیات گسسته از صفر تا صد (15 درس)






